- 您現(xiàn)在的位置:買賣IC網(wǎng) > PDF目錄371014 > MC145170 (Motorola, Inc.) PLL Frequency Synthesizer(PLL頻率發(fā)生器) PDF資料下載
參數(shù)資料
| 型號: | MC145170 |
| 廠商: | Motorola, Inc. |
| 英文描述: | PLL Frequency Synthesizer(PLL頻率發(fā)生器) |
| 中文描述: | 鎖相環(huán)頻率合成器(PLL頻率發(fā)生器) |
| 文件頁數(shù): | 5/14頁 |
| 文件大小: | 173K |
| 代理商: | MC145170 |
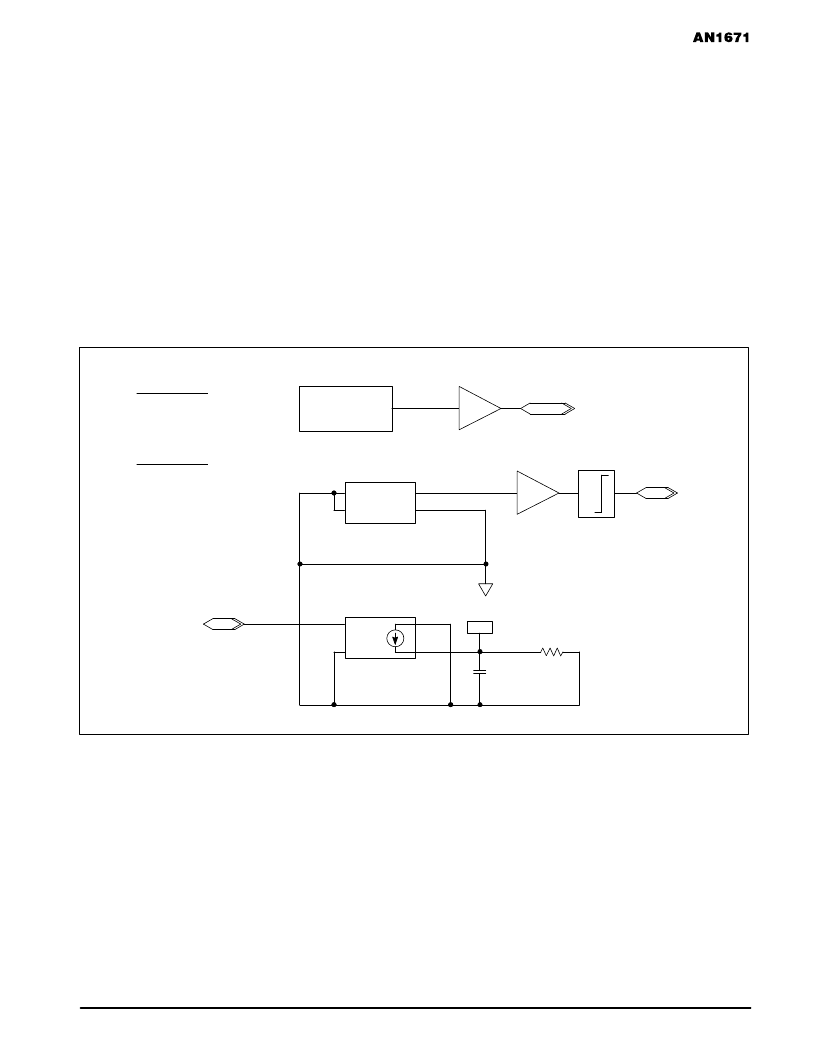
5
MOTOROLA RF/IF APPLICATIONS INFORMATION
The typical operation model parameters for transistors
end of this paper. For NRD and NRS, use 4/210 for the pmos
in the PDout driver, 4/66 for the nmos in the PDout driver,
4/300 for the pmos in the phiV and phiR buffers and 4/120 for
the nmos in the phiR and phiV buffers. M can be used to
establish the desired output drive of the transistors (from the
MC145170 specification).
The operation of the phase detector can be simulated for
different limits specified in the data sheet by modifying M for
the output transistors and the adjusting the value of the delay
element. For simulating devices with a specific minimum
pulse width, set the delay to the desired value. To observe the
effect of changing transistor drive levels, set M appropriately.
Additional Modifications
The examples shown below can be simulated using
MicroSim PSpice. In addition, the evaluation version of
PSpice can also be used for simulation if appropriate
adjustments to the models are made. These changes are
only two. The libraries provided with the evaluation PSpice
program do not include the primitive logic gates or the delay
element. They do however contain several of the “7400”
models which can be used for this application. The 7407
model can be used to implement the delay component and
the 7402 can be used for constructing the RSFF. While the
7407 needs to be modified for use as a delay element, the
7402 can be used as is or the “02” model can be edited to
reduce the propagation delay to that more in line with the
primitive NOR gate.
Two changes must be made to the 7407 to use it as a
delay element. The 7407 model must be modified to
eliminate the “open collector” reference and the “07” model
must be modified to contain the correct delay information.
This can be done to the existing model or the 7407 and 07
models can be copied to the user library, renamed and
modified to provide the special delay element. A simple text
editor can be used to edit the device models.
Out
VCOout
5 V
0 V
ctrl
1e99
R1
sin(tw*(fc*time+N*v(int)))
1
1E3
1e–6
+
PARAMETERS:
tw
fc
k1
6.283
6e6
1.26e7
PARAMETERS:
N
Qc
120
1e–6
IN+
IN–
OUT+
OUT–
evalue
sin(tw*((fc/N)*time+v(int)))
0
ctrl
IN+
IN–
gvalue
(k1/(tw*N))*v(ctrl)*Qc
G1
E1
C1
IC = 0 int
Figure 10.
Modeling the VCO
The VCO (Figure 10) is also modeled using Analog
Behavioral Modeling. The model used in the following
examples assumes a linear response however the control
voltage equation can be modified as desired. The circuit is
modeled as a sine generator controlled by the control
voltage. The sine generator can be modeled using the
EVALUE function or the ABM function. In Figure 10, the
EVALUE function is used to generate the divided output and
the ABM function is used for the undivided output. Either the
GVALUE or the ABM/I function can be used for the control
voltage.
The equation for the generator is:
e=sin(tw*((fc/N)*time+v(int))).
fc is defined as the output frequency when the control
voltage is zero. This is the expected VCO frequency before
frequency division. For the purpose of simulation, the counter
value, N, has been written into the equation to insure the
correlation between the modeled circuit and the
mathematical loop filter calculations. tw is pi times two;
additional decimal places can be added as needed. v(int) is
the control voltage effect and is defined in these examples
as:
v(int)=(k1/(tw*N))*v(cntl)*1e–10.
The value C1 in the schematic of the VCO can be
arbitrarily changed however the value must match that of Qc.
Qc determines the value of the current to be integrated by the
相關(guān)PDF資料 |
PDF描述 |
|---|---|
| MC14517BCL | Dual 64-Bit Static Shift Register |
| MC14517 | Dual 64-Bit Static Shift Register |
| MC14517BDWR2 | Dual 64-Bit Static Shift Register |
| MC14517BCP | Non-inverting High Speed MOSFET Driver with Active Pullup and Internal Regulator 5-SOT-23 |
| MC14517BDW | Dual 64-Bit Static Shift Register |
相關(guān)代理商/技術(shù)參數(shù) |
參數(shù)描述 |
|---|---|
| MC145170D1 | 制造商: 功能描述: 制造商:Motorola Inc 功能描述: 制造商:undefined 功能描述: |
| MC145170D2 | 功能描述:鎖相環(huán) - PLL PLL Synthesizer RoHS:否 制造商:Silicon Labs 類型:PLL Clock Multiplier 電路數(shù)量:1 最大輸入頻率:710 MHz 最小輸入頻率:0.002 MHz 輸出頻率范圍:0.002 MHz to 808 MHz 電源電壓-最大:3.63 V 電源電壓-最小:1.71 V 最大工作溫度:+ 85 C 最小工作溫度:- 40 C 封裝 / 箱體:QFN-36 封裝:Tray |
| MC145170D2R2 | 功能描述:鎖相環(huán) - PLL PLL Synthesizer RoHS:否 制造商:Silicon Labs 類型:PLL Clock Multiplier 電路數(shù)量:1 最大輸入頻率:710 MHz 最小輸入頻率:0.002 MHz 輸出頻率范圍:0.002 MHz to 808 MHz 電源電壓-最大:3.63 V 電源電壓-最小:1.71 V 最大工作溫度:+ 85 C 最小工作溫度:- 40 C 封裝 / 箱體:QFN-36 封裝:Tray |
| MC145170DT2 | 功能描述:鎖相環(huán) - PLL PLL Synthesizer RoHS:否 制造商:Silicon Labs 類型:PLL Clock Multiplier 電路數(shù)量:1 最大輸入頻率:710 MHz 最小輸入頻率:0.002 MHz 輸出頻率范圍:0.002 MHz to 808 MHz 電源電壓-最大:3.63 V 電源電壓-最小:1.71 V 最大工作溫度:+ 85 C 最小工作溫度:- 40 C 封裝 / 箱體:QFN-36 封裝:Tray |
| MC145170DT2R2 | 功能描述:IC SERIAL PLL FREQ SYNTH 16TSSOP RoHS:否 類別:集成電路 (IC) >> 時鐘/計時 - 時鐘發(fā)生器,PLL,頻率合成器 系列:- 標(biāo)準(zhǔn)包裝:39 系列:- 類型:* PLL:帶旁路 輸入:時鐘 輸出:時鐘 電路數(shù):1 比率 - 輸入:輸出:1:10 差分 - 輸入:輸出:是/是 頻率 - 最大:170MHz 除法器/乘法器:無/無 電源電壓:2.375 V ~ 3.465 V 工作溫度:0°C ~ 70°C 安裝類型:* 封裝/外殼:* 供應(yīng)商設(shè)備封裝:* 包裝:* |
發(fā)布緊急采購,3分鐘左右您將得到回復(fù)。