- 您現(xiàn)在的位置:買賣IC網(wǎng) > PDF目錄383075 > HSP50214B (Intersil Corporation) Programmable Downconverter PDF資料下載
參數(shù)資料
| 型號: | HSP50214B |
| 廠商: | Intersil Corporation |
| 英文描述: | Programmable Downconverter |
| 中文描述: | 可編程變頻器 |
| 文件頁數(shù): | 20/60頁 |
| 文件大小: | 573K |
| 代理商: | HSP50214B |
第1頁第2頁第3頁第4頁第5頁第6頁第7頁第8頁第9頁第10頁第11頁第12頁第13頁第14頁第15頁第16頁第17頁第18頁第19頁當(dāng)前第20頁第21頁第22頁第23頁第24頁第25頁第26頁第27頁第28頁第29頁第30頁第31頁第32頁第33頁第34頁第35頁第36頁第37頁第38頁第39頁第40頁第41頁第42頁第43頁第44頁第45頁第46頁第47頁第48頁第49頁第50頁第51頁第52頁第53頁第54頁第55頁第56頁第57頁第58頁第59頁第60頁
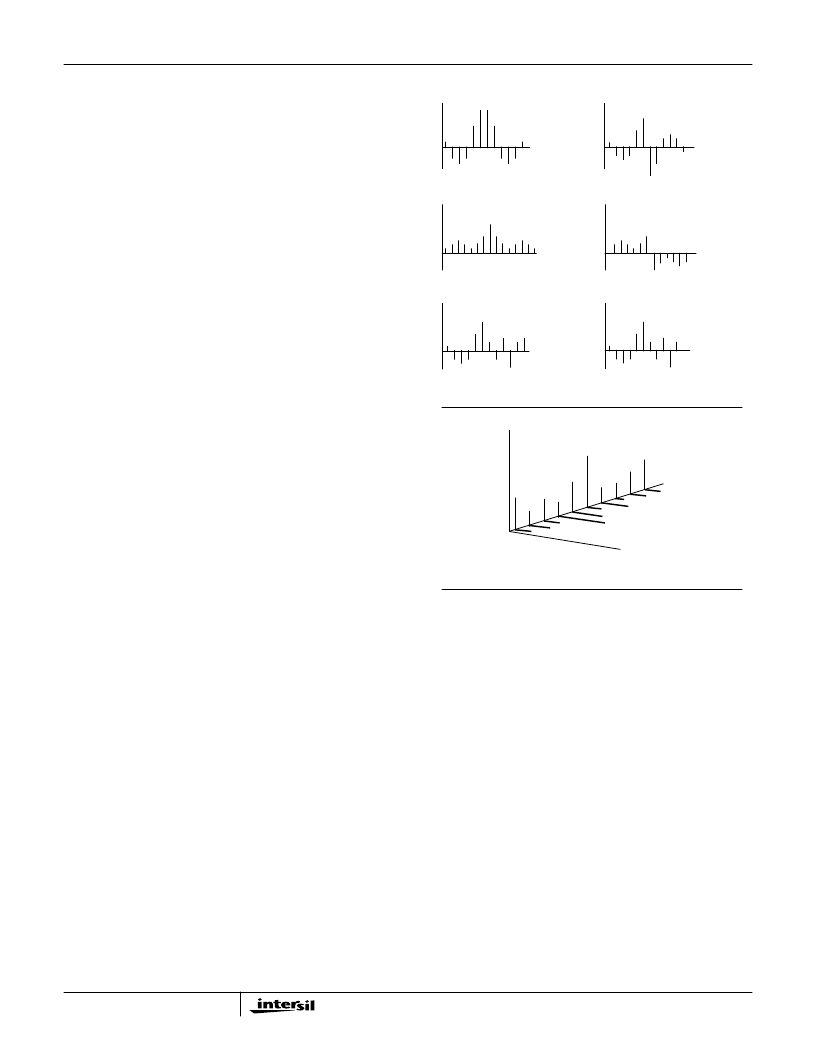
3-20
Additionally, the Programmable FIR filter provides for
decimation factors, R, from 1 to 16. The processing rate of
the Filter Compute Engine is PROCCLK. As a result, the
frequency of PROCCLK must exceed a minimum value to
ensure that a filter calculation is complete before the result is
required for output. In configurations which do not use
decimation, one input sample period is available for filter
calculation before an output is required. For configurations
which employ decimation, up to 16 input sample periods
may be available for filter calculation.
For real filter configurations, use Equation 11 to calculate the
number of taps available at a given input filter sample rate.
for real filters, and
for complex filters, where floor is defined as the integer
portion of a number; PROCCLK is the compute clock; f
SAMP
= the FIR input sample rate; R = Decimation Factor; SYM =
1 for symmetrical filter, 0 for asymmetrical filter; ODD# = 1
for an odd number of filter taps, 0 = an even number of taps.
Use Equation 12 to calculate the maximum input rate.
for real filters, and
for complex filters, where floor[x], PROCCLK, f
SAMP
, R =
Decimation Factor, SYM, and ODD# are defined as in
Equation 11.
Use Equation 13 to calculate the maximum output sample
rate for both real and complex filters.
The coefficients are 22 bits and are loaded using writes to
Control Words 128 through 255 (see Microprocessor Write
Section). For real filters, the same coefficients are used by I
and Q paths. If the filter is configured as a symmetric filter
using Control Word 17, Bit 9, then coefficients are loaded
starting with the center coefficient in Control Word 128 and
proceeding to last coefficient in Control Word 128+n. The
filter symmetry type can be set to even or odd symmetric,
and the number of filter coefficients can be even or odd, as
illustrated in Figure 20. Note that complex filters can also be
realized but are only allowed to be asymmetric. Only the
coefficients that are used need to be loaded.
Automatic Gain Control (AGC)
The AGC Section provides gain to small signals, after the
large signals and out-of-band noise have been filtered out, to
ensure that small signals have sufficient bit resolution in the
Resampling/Interpolating Halfband filters and the Output
Formatter. The AGC can also be used to manually set the
gain. The AGC optimizes the bit resolution for a variety of
input amplitude signal levels. The AGC loop automatically
adds gain to bring small signals from the lower bits of the 26-
bit programmable FIR filter output into the 16-bit range of the
TAPS
floor PROCCLK
SYM)
(
[
–
F
SAMP
R
)
]
(
)
R
]
–
(
)
1
+
(
=
(EQ. 11A)
SYM
)
ODD#
(
TAPS
floor (PROCCLK
F
SAMP
R
(
)
R
)
2]
–
=
(EQ. 11B)
(EQ. 12A)
F
SAMP
PROCCLK
(
)
R
( )
R
floor Taps
)
[
+
[
+
=
SYM
(
)
ODD#
(
)]
1
SYM
+
(
)
]]
(EQ. 12B)
F
SAMP
PROCCLK
(
)
R
( )
[
]
R
floor Taps
)
2
( )]
+
[
]
=
(EQ. 13)
F
FIROUT
F
SAMP
(
)
R
=
EVEN SYMMETRIC
EVEN TAP FILTER
ODD SYMMETRIC
EVEN TAP FILTER
EVEN SYMMETRIC
ODD TAP FILTER
ODD SYMMETRIC
ODD TAP FILTER
C0
CN-1
C
C
C0
CN-1
C0
CN-1
COEFFICIENT
NUMBER
COEFFICIENT
NUMBER
COEFFICIENT
NUMBER
COEFFICIENT
NUMBER
C
C
ASYMMETRIC
ODD TAP FILTER
C0
CN-1
COEFFICIENT
NUMBER
C
ASYMMETRIC
EVEN TAP FILTER
C0
CN-1
COEFFICIENT
NUMBER
C
COMPLEX FILTERS
C
Q(0)
C
I(N-1)
COEFFICIENT
NUMBER
I
REAL COEFFICIENT VALUE
C
C
Q(N-1)
REAL FILTERS
Definitions:
Even Symmetric: h(n) = h(N-n-1) for n = 0 to N-1
Odd Symmetric: h(n) = -h(N-n-1) for n = 0 to N-1
Asymmetric:
A filter with no coefficient symmetry.
Even Tap filter:
A filter where N is an even number.
Odd Tap filter:
A filter where N is an odd number.
Real Filter:
A filter implemented with real coefficients.
Complex Filters: A filter with quadrature coefficients.
FIGURE 20. DEMONSTRATION OF DIFFERENT TYPES OF
DIGITAL FIR FILTERS CONFIGURED IN THE
PROGRAMMABLE DOWNCONVERTER
C
V
C
Q
C
I
C0
CN
HSP50214B
相關(guān)PDF資料 |
PDF描述 |
|---|---|
| HSP50214BVC | Programmable Downconverter |
| HSP50214BVI | Programmable Downconverter |
| HT84 | ADSL Coupling Transformers |
| HT84-00594 | ADSL Coupling Transformers |
| HT8400594S | ADSL Coupling Transformers |
相關(guān)代理商/技術(shù)參數(shù) |
參數(shù)描述 |
|---|---|
| HSP50214B_07 | 制造商:INTERSIL 制造商全稱:Intersil Corporation 功能描述:Programmable Downconverter |
| HSP50214BVC | 功能描述:上下轉(zhuǎn)換器 120L MQFP COMTEMP 14-BIT PROGRAMMABLE DOWNCONVERTER 65MSPS RoHS:否 制造商:Texas Instruments 產(chǎn)品:Down Converters 射頻:52 MHz to 78 MHz 中頻:300 MHz LO頻率: 功率增益: P1dB: 工作電源電壓:1.8 V, 3.3 V 工作電源電流:120 mA 最大功率耗散:1 W 最大工作溫度:+ 85 C 安裝風(fēng)格:SMD/SMT 封裝 / 箱體:PQFP-128 |
| HSP50214BVCZ | 功能描述:上下轉(zhuǎn)換器 120L MQFP COMTEMP 14-BIT PROG DWNCNVRT RoHS:否 制造商:Texas Instruments 產(chǎn)品:Down Converters 射頻:52 MHz to 78 MHz 中頻:300 MHz LO頻率: 功率增益: P1dB: 工作電源電壓:1.8 V, 3.3 V 工作電源電流:120 mA 最大功率耗散:1 W 最大工作溫度:+ 85 C 安裝風(fēng)格:SMD/SMT 封裝 / 箱體:PQFP-128 |
| HSP50214BVI | 功能描述:上下轉(zhuǎn)換器 120L MQFP INDTEMP 14-BIT PROGRAMMABLE DOWNCONVERTER 65MSPS RoHS:否 制造商:Texas Instruments 產(chǎn)品:Down Converters 射頻:52 MHz to 78 MHz 中頻:300 MHz LO頻率: 功率增益: P1dB: 工作電源電壓:1.8 V, 3.3 V 工作電源電流:120 mA 最大功率耗散:1 W 最大工作溫度:+ 85 C 安裝風(fēng)格:SMD/SMT 封裝 / 箱體:PQFP-128 |
| HSP50214BVIZ | 功能描述:上下轉(zhuǎn)換器 120L MQFP INDTEMP 14-BIT PROG DWNCNVRT RoHS:否 制造商:Texas Instruments 產(chǎn)品:Down Converters 射頻:52 MHz to 78 MHz 中頻:300 MHz LO頻率: 功率增益: P1dB: 工作電源電壓:1.8 V, 3.3 V 工作電源電流:120 mA 最大功率耗散:1 W 最大工作溫度:+ 85 C 安裝風(fēng)格:SMD/SMT 封裝 / 箱體:PQFP-128 |
發(fā)布緊急采購,3分鐘左右您將得到回復(fù)。