- 您現(xiàn)在的位置:買賣IC網(wǎng) > PDF目錄373856 > μSAP70732-B03 (NEC Corp.) 8 Bit Single Chip Microcontrollers(8位單片微控制器) PDF資料下載
參數(shù)資料
| 型號(hào): | μSAP70732-B03 |
| 廠商: | NEC Corp. |
| 英文描述: | 8 Bit Single Chip Microcontrollers(8位單片微控制器) |
| 中文描述: | 8位單片機(jī)微控制器(8位單片微控制器) |
| 文件頁(yè)數(shù): | 25/166頁(yè) |
| 文件大?。?/td> | 713K |
| 代理商: | ΜSAP70732-B03 |
第1頁(yè)第2頁(yè)第3頁(yè)第4頁(yè)第5頁(yè)第6頁(yè)第7頁(yè)第8頁(yè)第9頁(yè)第10頁(yè)第11頁(yè)第12頁(yè)第13頁(yè)第14頁(yè)第15頁(yè)第16頁(yè)第17頁(yè)第18頁(yè)第19頁(yè)第20頁(yè)第21頁(yè)第22頁(yè)第23頁(yè)第24頁(yè)當(dāng)前第25頁(yè)第26頁(yè)第27頁(yè)第28頁(yè)第29頁(yè)第30頁(yè)第31頁(yè)第32頁(yè)第33頁(yè)第34頁(yè)第35頁(yè)第36頁(yè)第37頁(yè)第38頁(yè)第39頁(yè)第40頁(yè)第41頁(yè)第42頁(yè)第43頁(yè)第44頁(yè)第45頁(yè)第46頁(yè)第47頁(yè)第48頁(yè)第49頁(yè)第50頁(yè)第51頁(yè)第52頁(yè)第53頁(yè)第54頁(yè)第55頁(yè)第56頁(yè)第57頁(yè)第58頁(yè)第59頁(yè)第60頁(yè)第61頁(yè)第62頁(yè)第63頁(yè)第64頁(yè)第65頁(yè)第66頁(yè)第67頁(yè)第68頁(yè)第69頁(yè)第70頁(yè)第71頁(yè)第72頁(yè)第73頁(yè)第74頁(yè)第75頁(yè)第76頁(yè)第77頁(yè)第78頁(yè)第79頁(yè)第80頁(yè)第81頁(yè)第82頁(yè)第83頁(yè)第84頁(yè)第85頁(yè)第86頁(yè)第87頁(yè)第88頁(yè)第89頁(yè)第90頁(yè)第91頁(yè)第92頁(yè)第93頁(yè)第94頁(yè)第95頁(yè)第96頁(yè)第97頁(yè)第98頁(yè)第99頁(yè)第100頁(yè)第101頁(yè)第102頁(yè)第103頁(yè)第104頁(yè)第105頁(yè)第106頁(yè)第107頁(yè)第108頁(yè)第109頁(yè)第110頁(yè)第111頁(yè)第112頁(yè)第113頁(yè)第114頁(yè)第115頁(yè)第116頁(yè)第117頁(yè)第118頁(yè)第119頁(yè)第120頁(yè)第121頁(yè)第122頁(yè)第123頁(yè)第124頁(yè)第125頁(yè)第126頁(yè)第127頁(yè)第128頁(yè)第129頁(yè)第130頁(yè)第131頁(yè)第132頁(yè)第133頁(yè)第134頁(yè)第135頁(yè)第136頁(yè)第137頁(yè)第138頁(yè)第139頁(yè)第140頁(yè)第141頁(yè)第142頁(yè)第143頁(yè)第144頁(yè)第145頁(yè)第146頁(yè)第147頁(yè)第148頁(yè)第149頁(yè)第150頁(yè)第151頁(yè)第152頁(yè)第153頁(yè)第154頁(yè)第155頁(yè)第156頁(yè)第157頁(yè)第158頁(yè)第159頁(yè)第160頁(yè)第161頁(yè)第162頁(yè)第163頁(yè)第164頁(yè)第165頁(yè)第166頁(yè)
25
CHAPTER 1 OVERVIEW
(5) Quantization and zigzag scan
It is said that the human eye can barely recognize changes in high-frequency components but can easily
recognize the most subtle changes in low-frequency components. To increase the compression ratio,
JPEG compression divides low-frequency components by a small value and high-frequency components
by a greater value. This processing is called quantization. To expand compressed data, the data is
multiplied by the same value by which it was divided (reverse quantization). However, the data cannot
be fully restored by applying quantization and reverse quantization (cannot be reversed). This is because,
when data is quantized, only the quotient resulting from division is used as information, the remainder
being ignored. In this way, the JPEG standard enables an increase in the compression ratio without visibly
degrading the image.
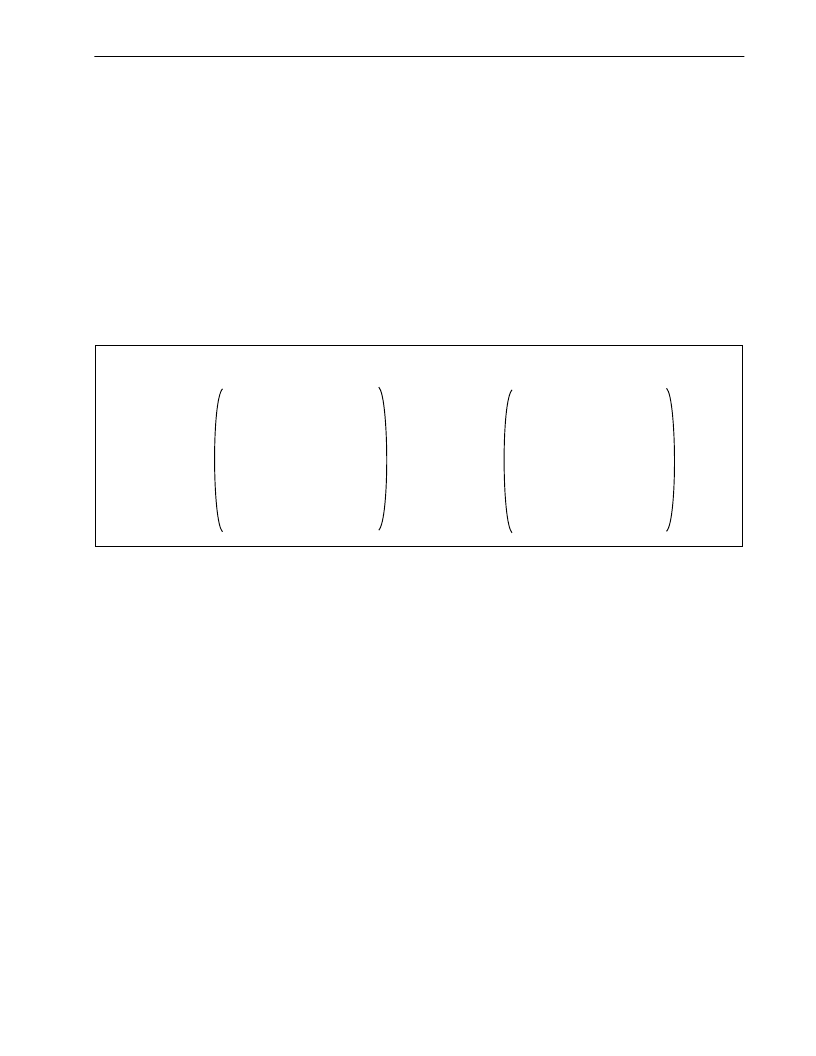
Figure 1-8. Quantized Matrix and Quantization
Data obtained by applying DCT to a block of the original image is notable in that the data of the Y component
differs from that of the Cb/Cr component. Therefore, JPEG uses two types of quantized matrixes for the
Y and Cb/Cr components, respectively (in some cases, only one quantized matrix is used). These
quantized matrixes can be defined independently for each image (JPEG file). Information relating to these
quantized matrixes is stored as a DQT segment in the header of the JPEG file.
As shown by the example in Figure 1-8, if most of the values in the obtained matrix are 0, the information
that “there is a sequence of n zeroes followed by a value that is not zero” is interpreted to increase the
compression rate. The JPEG standard refers to this “sequence of zeroes” as “the length of zero run.”
The non-zero values in the matrix obtained as a result of quantization gather in the upper left part of the
matrix most of the time. For this reason, the length of the zero run is counted by JPEG in the sequence
illustrated below (zigzag scan).
Example of quantized matrix
Example of quantized 8 x 8 matrix
8 16 19 22 26 27 29 34
16 16 22 24 27 29 34 37
19 22 26 27 29 34 34 38
22 22 26 27 29 34 37 40
22 26 27 29 32 35 40 48
26 27 29 32 35 40 48 58
26 27 29 34 38 46 56 69
27 29 35 38 46 56 69 83
43 -9 0
1
0
0
0 0
-8 -4 0
1
0
0
0 0
0
3
2
0 -1
0
0 0
-1 1
0
0
0
0
0 0
0
1
0
0
0
0
0 0
0
0
0
0
0
0
0 0
0
0
0
0
0
0
0 0
0
0
0
0
0
0
0 0
Q(i j) =
相關(guān)PDF資料 |
PDF描述 |
|---|---|
| AADG812YRU | 0.5 CMOS 1.65 V to 3.6 V Quad SPST Switches |
| AC1226 | Micropower Thermocouple Cold Junction Compensator(微功耗熱電耦冷節(jié)點(diǎn)補(bǔ)償) |
| AC2626 | General Purpose Temperture Probe(通用溫度探測(cè)器) |
| AC2626J | General Purpose Temperature Probe |
| AC2626K | General Purpose Temperature Probe |
相關(guān)代理商/技術(shù)參數(shù) |
參數(shù)描述 |
|---|---|
| SAP-8511250B300 | 制造商:Seiko Instruments Inc (SII) 功能描述: |
| SAPM01N | 制造商:SANKEN 制造商全稱:Sanken electric 功能描述:silicon power MOSFET |
| SAPPBU10 | 制造商:Panduit Corp 功能描述:ZONE CORD, CAT 6A FTP SOLID PLENUM BLUE - Cable Rools/Shrink Tubing |
| SAPPBU100 | 制造商:Panduit Corp 功能描述:ZONE CORD, CAT 6A FTP SOLID PLENUM BLUE - Cable Rools/Shrink Tubing |
| SAPPBU110 | 制造商:Panduit Corp 功能描述:ZONE CORD, CAT 6A FTP SOLID PL 制造商:Panduit Corp 功能描述:ZONE CORD, CAT 6A FTP SOLID PLENUM BLUE - Cable Rools/Shrink Tubing |
發(fā)布緊急采購(gòu),3分鐘左右您將得到回復(fù)。