參數(shù)資料
型號(hào)： L6615N
廠商： 意法半導(dǎo)體
英文描述： HIGH/LOW SIDE LOAD SHARE CONTROLLER
中文描述： 高/低側(cè)負(fù)載共享控制器
文件頁(yè)數(shù)： 12/20頁(yè)
文件大小： 392K
代理商： L6615N
L6615
12/20
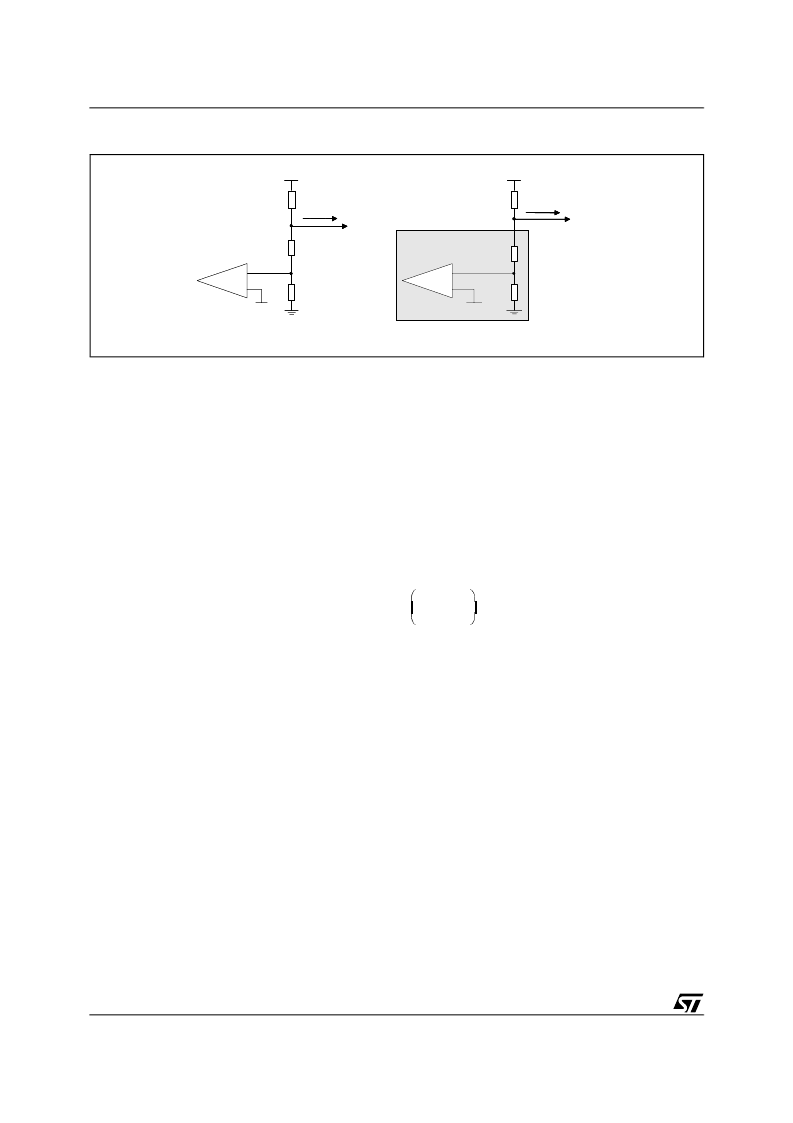
Figure 12. ADJ network
To set the R
ADJ
value it is necessary to know the tolerance required of the power supply output voltage
(V
OUT
±
V
O
); the maximum difference between master and slave output voltage is 2*
V
O
and this amount
represents the voltage that the L6615 must be able to correct.
Now two different approaches are feasible depending on whether the SMPS (whose output current must
be shared) has to be completely designed or it is an "off the shelf" component and only the current sharing
section must be designed.
In the first case, the adjustment resistor (R
ADJ
) can be considered as a fraction of the high resistor of the
feedback divider R
H
(see fig.12.a): typically the first step consist of fixing the current flowing, under steady
state condition, through the feedback divider I
FB
; by choosing the value for R
2
:
we will have:
It can be an useful rule of thumb to use R
ADJ
lower than (or equal to) one tenth of R1, considering that, in
worst case condition, it will be:
This value must not exceed the one indicated in the "Electrical characteristic section" but this is very easy
to meet, as one can easily see by using sensible values for
V
OUT
and R
2
.
In the second case (fig 12.b), the feedback divider has been already designed by the SMPS manufacturer
and it is not possible to modify it: the design of R
ADJ
must be done to make the L6615 able to correct the
maximum spread without significantly shifting the SMPS regulation point. A minimum R
ADJ
value can be
found by:
where I
ADJ(max)
is 8mA.
Especially for low voltage output buses it is important to avoid adjustment network saturation; the design
must satisfy the following relationship:
where V
ADJ(MIN)
can be found in the "Electrical characteristic section" for different I
ADJ
values.
V
OUT
V
REF
POWER SUPPLY
R
ADJ
E/A
ADJ pin
I
ADJ
V
OUT
V
REF
R
ADJ
E/A
ADJ pin
I
ADJ
R
1
R
2
a)
b)
Off the shelf
to L6615
to L6615
I
FB
V
R
2
--------------
=
R
H
R
1
R
ADJ
+
V
V
REF
--------------
1
–
R
2
=
=
I
ADJ max
)
V
R
ADJ
------------------
=
R
ADJ min
)
V
I
ADJ max
)
-------------------------
=
V
OUT
R
ADJ
I
ADJ
I
FB
+
(
)
V
ADJ MIN
)
>
–
相關(guān)PDF資料
PDF描述
L6660 MILLI-ACTUATOR DRIVER
L6668 SMART PRIMARY CONTROLLER
L6668TR SMART PRIMARY CONTROLLER
L6710 6 BIT PROGRAMMABLE DUAL-PHASE CONTROLLER WITH DYNAMIC VID MANAGEMENT
L6712A TWO-PHASE INTERLEAVED DC/DC CONTROLLER
相關(guān)代理商/技術(shù)參數(shù)
參數(shù)描述
L6622-01 制造商:HAMAMATSU 制造商全稱:Hamamatsu Corporation 功能描述:130 KV MICROFOCUS X-RAY SOURCE
L-663 制造商:RHOMBUS-IND 制造商全稱:Rhombus Industries Inc. 功能描述:CURRENT SENSE INDUCTOR
L6-6330 制造商: 功能描述: 制造商:undefined 功能描述:
L6660 制造商:STMICROELECTRONICS 制造商全稱:STMicroelectronics 功能描述:MILLI-ACTUATOR DRIVER
L6668 功能描述:電流型 PWM 控制器 SMART PRIMARY CONTROLLER RoHS:否 制造商:Texas Instruments 開(kāi)關(guān)頻率:27 KHz 上升時(shí)間: 下降時(shí)間: 工作電源電壓:6 V to 15 V 工作電源電流:1.5 mA 輸出端數(shù)量:1 最大工作溫度:+ 105 C 安裝風(fēng)格:SMD/SMT 封裝 / 箱體:TSSOP-14
發(fā)布緊急采購(gòu)，3分鐘左右您將得到回復(fù)。

采購(gòu)需求

(若只采購(gòu)一條型號(hào)，填寫(xiě)一行即可)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

*型號(hào) *數(shù)量 廠商 批號(hào) 封裝
添加更多采購(gòu)

我的聯(lián)系方式

*
*
*