- 您現(xiàn)在的位置：買賣IC網(wǎng) > PDF目錄24938 > 0805ZC103MA74A (AVX Corporation) General Specifications PDF資料下載
參數(shù)資料
| 型號： | 0805ZC103MA74A |
| 廠商： | AVX Corporation |
| 英文描述： | General Specifications |
| 中文描述： | 一般規(guī)格 |
| 文件頁數(shù)： | 8/20頁 |
| 文件大?。?/td> | 338K |
| 代理商： | 0805ZC103MA74A |
56
General Description
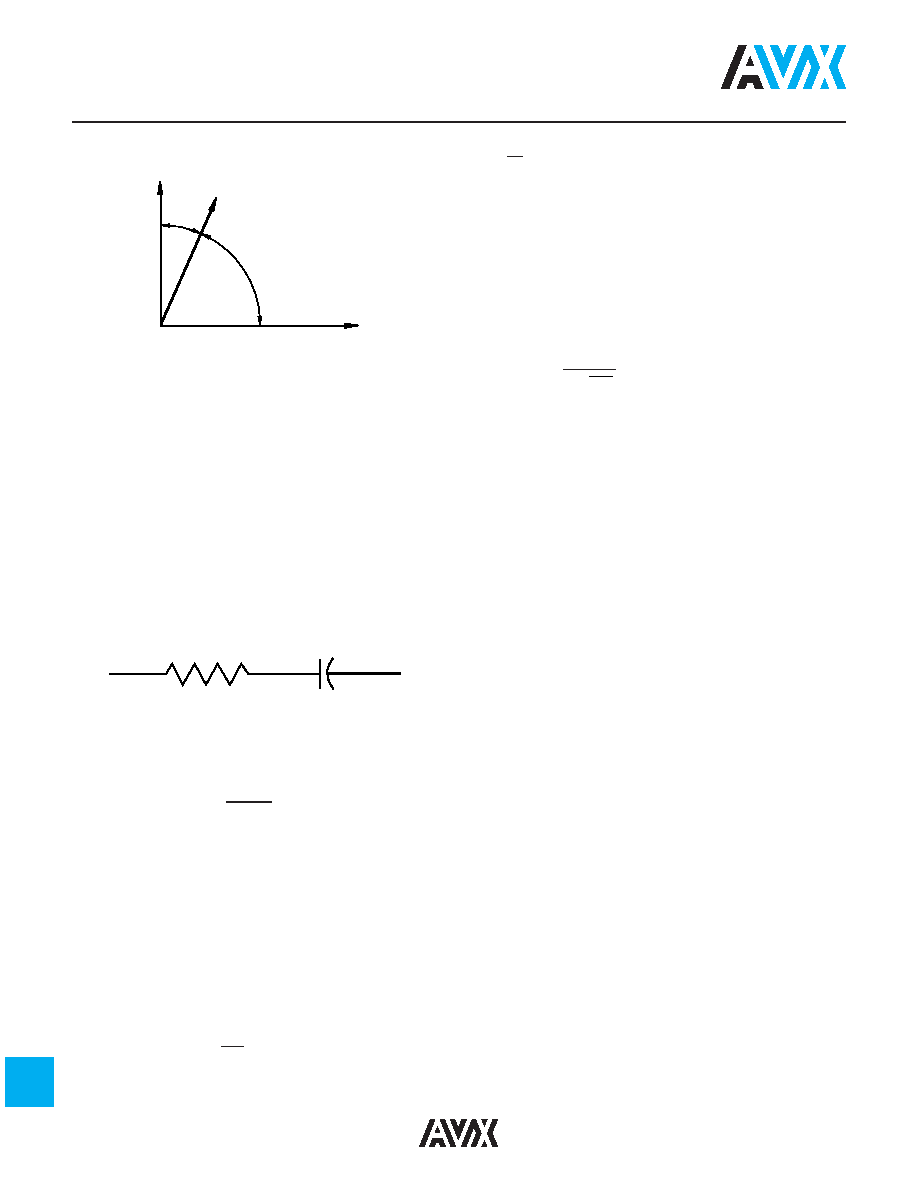
In practice the current leads the voltage by some other
phase angle due to the series resistance R
S. The comple-
ment of this angle is called the loss angle and:
Power Factor (P.F.) = Cos
f or Sine
Dissipation Factor (D.F.) = tan
for small values of
the tan and sine are essentially equal
which has led to the common interchangeability of the two
terms in the industry.
Equivalent Series Resistance – The term E.S.R. or
Equivalent Series Resistance combines all losses both
series and parallel in a capacitor at a given frequency so
that the equivalent circuit is reduced to a simple R-C series
connection.
Dissipation Factor – The DF/PF of a capacitor tells what
percent of the apparent power input will turn to heat in the
capacitor.
Dissipation Factor =
E.S.R.
= (2
π fC) (E.S.R.)
X
C
The watts loss are:
Watts loss = (2
π fCV2) (D.F.)
Very low values of dissipation factor are expressed as their
reciprocal for convenience. These are called the “Q” or
Quality factor of capacitors.
Parasitic Inductance – The parasitic inductance of capac-
itors is becoming more and more important in the decou-
pling of today’s high speed digital systems. The relationship
between the inductance and the ripple voltage induced on
the DC voltage line can be seen from the simple inductance
equation:
V = L di
dt
The
seen in current microprocessors can be as high as
0.3 A/ns, and up to 10A/ns. At 0.3 A/ns, 100pH of parasitic
inductance can cause a voltage spike of 30mV. While this
does not sound very drastic, with the Vcc for microproces-
sors decreasing at the current rate, this can be a fairly large
percentage.
Another important, often overlooked, reason for knowing
the parasitic inductance is the calculation of the resonant
frequency. This can be important for high frequency, by-
pass capacitors, as the resonant point will give the most
signal attenuation. The resonant frequency is calculated
from the simple equation:
fres =
1
2
LC
Insulation Resistance – Insulation Resistance is the
resistance measured across the terminals of a capacitor
and consists principally of the parallel resistance R P shown
in the equivalent circuit. As capacitance values and hence
the area of dielectric increases, the I.R. decreases and
hence the product (C x IR or RC) is often specified in ohm
faradsor more commonly megohm-microfarads. Leakage
current is determined by dividing the rated voltage by IR
(Ohm’s Law).
Dielectric Strength – Dielectric Strength is an expression
of the ability of a material to withstand an electrical stress.
Although dielectric strength is ordinarily expressed in volts, it
is actually dependent on the thickness of the dielectric and
thus is also more generically a function of volts/mil.
Dielectric Absorption – A capacitor does not discharge
instantaneously upon application of a short circuit, but
drains gradually after the capacitance proper has been dis-
charged. It is common practice to measure the dielectric
absorption by determining the “reappearing voltage” which
appears across a capacitor at some point in time after it has
been fully discharged under short circuit conditions.
Corona – Corona is the ionization of air or other vapors
which causes them to conduct current. It is especially
prevalent in high voltage units but can occur with low voltages
as well where high voltage gradients occur. The energy
discharged degrades the performance of the capacitor and
can in time cause catastrophic failures.
di
dt
I (Ideal)
I (Actual)
Phase
Angle
Loss
Angle
V
IR
s
f
E.S.R.
C
相關(guān)PDF資料 |
PDF描述 |
|---|---|
| 0805 | Case No. 0805 Device |
| 0805-T | Case No. 0805 Device |
| 0806-5400-01 | DOCSIS 2.0 Diplexer Filter |
| 0806-5400-03 | EuroDOCSIS 2.0 Diplexer Filter w/surge protection |
| 0806-5400-01 | DOCSIS 2.0 Diplexer Filter |
相關(guān)代理商/技術(shù)參數(shù) |
參數(shù)描述 |
|---|---|
| 0805ZC103MAT2A | 功能描述:多層陶瓷電容器MLCC - SMD/SMT 10volts 0.01uF 20% X7R RoHS:否 制造商:American Technical Ceramics (ATC) 電容:10 pF 容差:1 % 電壓額定值:250 V 溫度系數(shù)/代碼:C0G (NP0) 外殼代碼 - in:0505 外殼代碼 - mm:1414 工作溫度范圍:- 55 C to + 125 C 產(chǎn)品:Low ESR MLCCs 封裝:Reel |
| 0805ZC103MAT4A | 功能描述:多層陶瓷電容器MLCC - SMD/SMT 10volts 0.01uF 20% X7R RoHS:否 制造商:American Technical Ceramics (ATC) 電容:10 pF 容差:1 % 電壓額定值:250 V 溫度系數(shù)/代碼:C0G (NP0) 外殼代碼 - in:0505 外殼代碼 - mm:1414 工作溫度范圍:- 55 C to + 125 C 產(chǎn)品:Low ESR MLCCs 封裝:Reel |
| 0805ZC104JAT2A | 功能描述:多層陶瓷電容器MLCC - SMD/SMT 10volts 0.1uF 5% X7R RoHS:否 制造商:American Technical Ceramics (ATC) 電容:10 pF 容差:1 % 電壓額定值:250 V 溫度系數(shù)/代碼:C0G (NP0) 外殼代碼 - in:0505 外殼代碼 - mm:1414 工作溫度范圍:- 55 C to + 125 C 產(chǎn)品:Low ESR MLCCs 封裝:Reel |
| 0805ZC104JAZ2A | 功能描述:多層陶瓷電容器MLCC - SMD/SMT 0805 0.1uF 10volts X7R 5% RoHS:否 制造商:American Technical Ceramics (ATC) 電容:10 pF 容差:1 % 電壓額定值:250 V 溫度系數(shù)/代碼:C0G (NP0) 外殼代碼 - in:0505 外殼代碼 - mm:1414 工作溫度范圍:- 55 C to + 125 C 產(chǎn)品:Low ESR MLCCs 封裝:Reel |
| 0805ZC104KAT2A | 功能描述:多層陶瓷電容器MLCC - SMD/SMT 0805 0.1uF 10volts X7R 10% RoHS:否 制造商:American Technical Ceramics (ATC) 電容:10 pF 容差:1 % 電壓額定值:250 V 溫度系數(shù)/代碼:C0G (NP0) 外殼代碼 - in:0505 外殼代碼 - mm:1414 工作溫度范圍:- 55 C to + 125 C 產(chǎn)品:Low ESR MLCCs 封裝:Reel |
發(fā)布緊急采購，3分鐘左右您將得到回復(fù)。